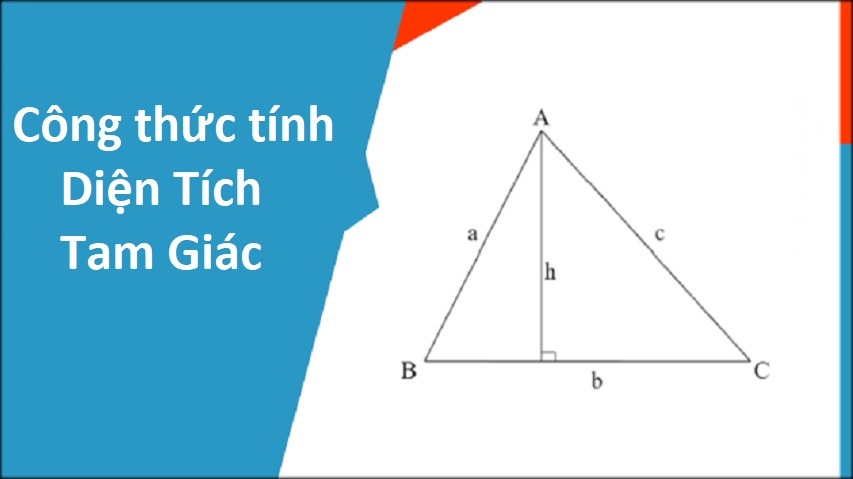
Toán là một môn học vô cùng cần thiết và không thể thiếu đối với chúng ta. Hầu hết các lĩnh vực, hoạt động hằng ngày điều cần đến toán. Đây là một môn học rất hay và chứa đựng rất nhiều điều thú vị. Để có thể học tốt môn này, điều đầu tiên các bạn cần phải nắm vững là các công thức toán học. Nhắc đến các công thức thì có rất nhiều: Công thức đạo hàm, lượng giác, nguyên hàm,… và các công thức liên quan đến hình học.
Một trong các công thức hình học bạn cần phải nhớ chính là công thức tính diện tích tam giác. Tam giác thì có rất nhiều loại nên để tính diện tích được, các bạn cần phải biết áp dụng đúng các công thức. Để có thể xử lý tốt các bài tập liên quan đến tính diện tích tam giác, không còn cách nào khác hơn là phải thuộc và biết áp dụng từng công thức vào từng dạng bài tập khác nhau. Trong bài viết này, mình sẽ chia sẻ đến các bạn công thức tính diện tích tam giác chuẩn và chính xác.
Mục Lục
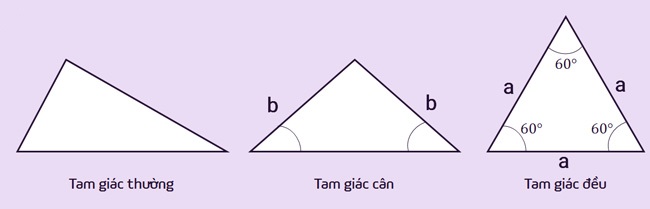
Phân loại tam giác
– Tam giác thường: Là tam giác có độ dài các cạnh và số đo các góc trong khác nhau
– Tam giác cân: Là tam giác có hai cạnh bất kỳ bằng nhau. Hai cạnh này tạo thành một góc gọi là góc đỉnh. Hai góc còn lại là góc đáy và có số đo góc trong bằng nhau.
– Tam giác đều: Là tam giác có 3 cạnh và 3 góc trong bằng nhau (Có số đo là 60 độ)
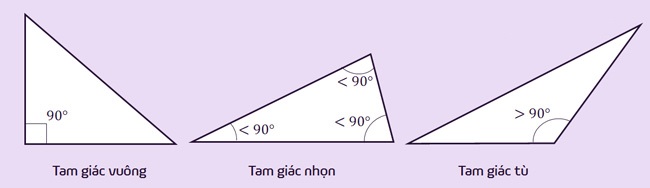
– Tam giác vuông: Là tam giác có một góc trong bằng 90 độ. Cạnh đối diện với góc vuông gọi là cạnh huyền. Hai cạnh còn lại gọi là hai cạnh góc vuông.
– Tam giác nhọn: Là tam giác có 3 góc trong đều nhỏ hơn 90 độ.
– Tam giác tù: Là tam giác có một góc trong lớn hơn 90 độ
Các công thức tính diện tích tam giác
1. Công thức tính diện tích tam giác thường
– Giả sử tam giác cần tính là ABC, có:
- Độ dài cạnh AB = c
- Độ dài cạnh AC = b
- Độ dài cạnh BC = a
- Độ dài đường cao từ đỉnh A= ha (Độ dài đường cao từ đỉnh B= hb, Độ dài đường cao từ đỉnh C= hc )
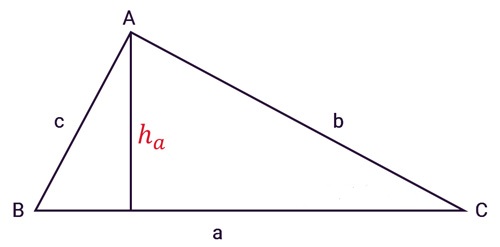
– Công thức tính diện tích tam giác thường khi biết chiều dài đường cao và chiều dài cạnh đáy tam giác.
[pmath size=16]{S_{ABC}} = {1}/{2}a.{h_a} = {1}/{2}b.{h_b} = {1}/{2}c.{h_c}[/pmath]
– Công thức tính diện tích tam giác thường khi biết hai cạnh và sin của góc hợp bởi hai cạnh đó.
[pmath size=16]{S_{ABC}} = {1}/{2}a.b.sin C = {1}/{2}a.c.sin B = {1}/{2}b.c.sin A[/pmath]
– Sử dụng công thức Heron:
[pmath size=16]S = \sqrt {p\( {p – a})({p – b} \)\( {p – c} \)}[/pmath]
Trong đó: [pmath size=16]p = {1}/{2}( {a + b + c} \)[/pmath] Với p là nửa chu vi của tam giác.
– Công thức tính diện tích tam giác thường khi biết bán kính đường tròn ngoại tiếp tam giác.
[pmath size=16]{S_{ABC}} = {abc}/{4R}[/pmath]
Trong đó: R là bán kính đường tròn ngoại tiếp tam giác
– Công thức tính diện tích tam giác thường khi biết bán kính đường tròn nội tiếp tam giác.
[pmath size=16]{S_{ABC}} = p.r[/pmath]
Trong đó: r là bán kính đường tròn nội tiếp
– Hoặc các bạn có thể sử dụng công thức sau:
[pmath size=16]{S_{ABC}} = 2.{R^2}.sin A.sin B.sin C[/pmath]
2. Công thức tính diện tích tam giác cân
– Cho tam giác cân ABC có:
- AB = AC = b
- BC = a
- Độ dài đường cao từ đỉnh A= ha
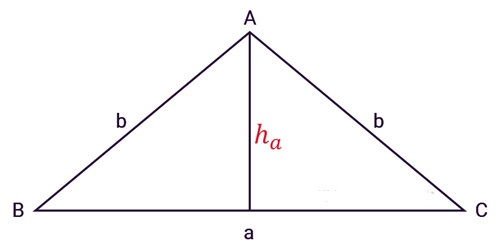
– Áp dụng công thức sau:
[pmath size=16]{S_{ABC}} = {1}/{2}a.{h_a}[/pmath]
3. Công thức tính diện tích tam giác đều
– Cho tam giác đều ABC có:
- AB = AC = BC = a
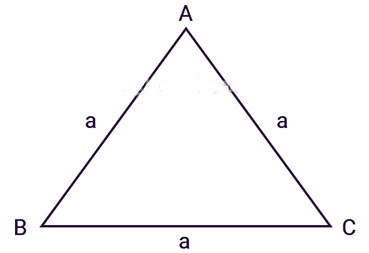
– Áp dụng công thức:
[pmath size=16]{S_{ABC}} = {a^2}{{\sqrt 3 }}/{4}[/pmath]
4. Công thức tính diện tích tam giác vuông
– Cho tam giác vuông ABC có:
- AB = a
- BC = b
- Góc B = 90 độ
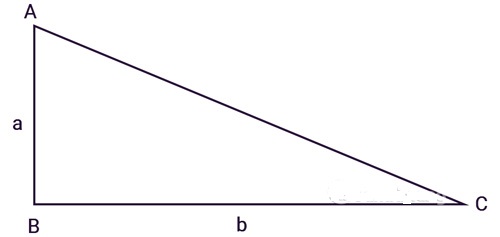
– Áp dụng công thức:
[pmath size=16]{S_{ABC}} = {1}/{2}a.b[/pmath]
5. Công thức tính diện tích tam giác vuông cân
– Cho tam giác vuông cân ABC có:
- AB = AC = a
- Góc A = 90 độ
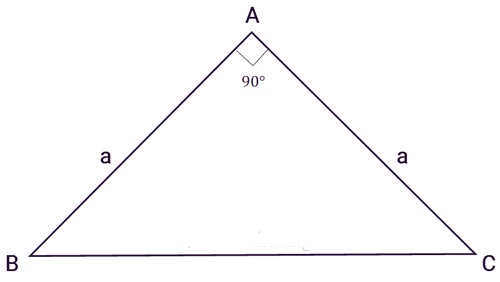
– Áp dụng công thức sau:
[pmath size=16]{S_{ABC}} = {1}/{2}a^2[/pmath]
Lời kết
Trên đây là các công thức tính diện tích tam giác được sử dụng nhiều nhất. Nếu bạn nào có công thức tính diện tích tam giác mới thì vui lòng để lại bình luận bên dưới để cho mọi người cùng tham khảo và sử dụng. Chúc các bạn thành công!